octave tutotial 3

Control Statements: for, while, if statement

• for loop

   v = zeros(10, 1)
   v =
  
      0
      0
      0
      0
      0
      0
      0
      0
      0
      0
     
   for j = 1 : 10,
      v(i) = 2 ^ i;
   end;
  
   v
   v = 
  
      2
      4
      8
     16
     32
     64
    128
    256
    512
   1024
  

• for loop 2

  好還要更好 ! 就是一直修正~~~ 接下來的 code example 都會直接把 octave code 畫面剪下來貼上去 所以可以看的到 » 唷唷

   >> indices = 1 : 10;
   >> indices
   indices =
     
       1    2    3    4    5    6    7    8    9   10
     
   >> for i = indices,
       disp(i);
      end;
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
  

• while

   >> v
   v =
     
         2
         4
         8
        16
        32
        64
       128
       256
       512
      1024
     
   >> i = 1;
   >> while i <=5,
       v(i) = 100;
       i = i + 1;
      end;
   >> v
   v =
     
       100
       100
       100
       100
       100
        64
       128
       256
       512
      1024
     
  

• if, break

   >> v
   v =
     
       100
       100
       100
       100
       100
        64
       128
       256
       512
      1024
     
   >> i = 1;
   >> while true,
        v(i) = 999;
        i = i + 1;
        if i == 6,
          break;
        end;
      end;
     
   >> v
   v =
     
       999
       999
       999
       999
       999
        64
       128
       256
       512
      1024
  
  

• else if

   >> v(1) = 2
   v =
  
      2
    999
    999
    999
    999
     64
    128
    256
    512
   1024
  
   >> if v(1) == 1,
        disp('The value is one ');
      elseif v(1) == 2,
        disp('The value is two');
      else
        disp('The value is not one or two.');
      end;
   The value is two
  
  

• function

  • 新建一個檔案， 命名 [functionName].m

     % squareThisNumber.m
       
     function y = squareThisNumber(x)
     y = x^2
    

  • cd 到 有這支檔案的路徑

  • EX: E:\Coursera\Machine_Learning\_octave_exercise

     >> ls
      Volume in drive E is DATA
      Volume Serial Number is F859-A48F
          
      Directory of E:\Coursera\Machine_Learning\_octave_exercise
          
     [.]                  [..]                 squareThisNumber.m   test.txt
                    2 File(s)            238 bytes
                    2 Dir(s)  961,864,597,504 bytes free
    

  • 直接在 octave cmd 裡呼叫使用

     >> squareThisNumber(2)
     y =  4
     ans =  4
    

• Octave search path
  • 加入path 讓 octave cmd 可以無痛讀取相關檔案
  • EX:

    >> addpath('E:\Coursera\Machine_Learning\_octave_exercise')
    >>
    >> cd 'C:\'
    >> squareThisNumber(5)
    y =  25
    ans =  25
    

• costFunctionJ
  • costFunctionJ.m:

  • 複習照片:

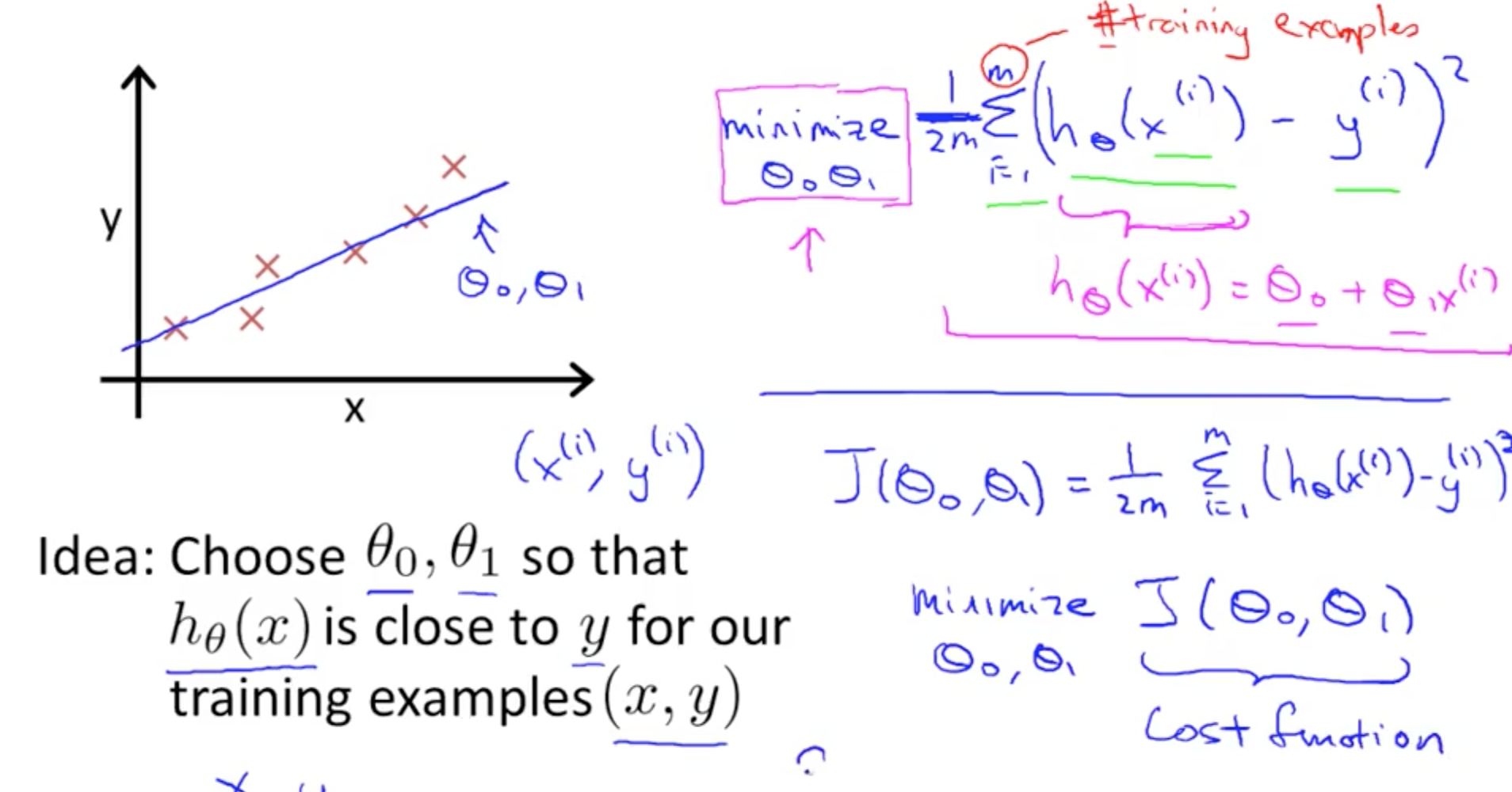
     function J = costFunctionJ(X, y, theta)
       
     % X is the "design matrix" containing our training examples.
     % y is the class labels
          
     m = size(X, 1); % number of training examples
     predictions = X * theta; % predictions of hypothesis on all m examples
     sqrError = (predictions - y) .^2 % squared errors
       
     J = 1/(2 * m) * sum(sqrErrors);
    

  • 跑跑看 costFunctionJ:

     >> X
     X =
          
        1   1
        1   2
        1   3
          
     >> y = [1; 2; 3]
     y =
          
        1
        2
        3
          
     >> theta = [0; 1]
     theta =
          
        0
        1
          
     >> j = costFunctionJ(X, y, theta)
     j = 0  % 0 代表 完美的找出theta !!!
    

Vectorization

• Vectorization example

   hθ(x) = ∑(j=0, n)  θj * xj
           
         = θ^T * x
  
        | θ0 |        | x0 |
   θ =  | θ1 |   x =  | x1 |            
        | θ2 |,       | x2 |      
  

  • Unvectorized implementation

      prediction = 0.0;
      for j = i : n+1,
         prediction = prediction + theta(j) * x(j)
      end;
    

  • vectorized implementation

      prediction = theta' * x;
    

• C ++ Vectorization example

  • Unvectorized implementation

      double prediction = 0.0;
      for( int j = 0; j <=n ; j++)
         prediction += theta[j] * x[j];
    

  • vectorized implementation

      double prediction 
       = theta.transpose() * x;
    

• Gradient descent

   θj := θj - α * 1/m * ∑ ( hθ * ( x^(i) ) - y^(i) )* xj^(i)  # [∑ i=1, m]
   (for all j)
  

  ---

  Simultaneous update :

   θ0 := θ0 - α * 1/m * ∑ ( hθ * ( x^(i) ) - y^(i) )* x0^(i)   # [∑ i=1, m]    
   θ1 := θ1 - α * 1/m * ∑ ( hθ * ( x^(i) ) - y^(i) )* x1^(i)   # [∑ i=1, m]    
   θ2 := θ2 - α * 1/m * ∑ ( hθ * ( x^(i) ) - y^(i) )* x2^(i)   # [∑ i=1, m]